Algoritma
Deteksi Persentase Kemiripan Teks Menggunakkan Algoritma Cosine Similarity
Penerapan Algoritma Elgamal Untuk Enkripsi Dan Dekripsi File Teks
Sistem Pakar Untuk Mendiagnosa Penyakit Kulit Pada Manusia Menggunakkan Metode Certainty Factor (CF)
Penerapan algoritma nearest neighbor untuk memprediksi data pengajuan pinjaman calon nasabah baru
Pengelompokkan data menggunakkan algoritma k-means clustering
Sistem Pendukung Keputusan Seleksi Karyawan Baru Menggunakkan Algoritma Topsis
Implementasi Program Algoritma RSA Untuk Enkripsi Dan Dekripsi File Teks
Perhitungan Metode Fuzzy AHP Dalam Pemilihan Karyawan Terbaik
React Native
Software

Sejarah Algoritma RSA
Algortima RSA pertama kali dijabarkan sekitar tahun 1976 oleh 3 orang dari Massachusetts Institute of Technology yaitu :
- Ron Rivest
- Adi Shamir
- Len Adleman
Penemuan Clifford Cocks tidak terungkap hingga tahun 1997 karena alasan top-secret classification. Algoritma RSA dipatenkan oleh Massachusetts Institute of Technology pada tahun 1983 di Amerika Serikat sebagai US patent 4405829. Paten tersebut berlaku hingga 21 September 2000. Setelah bulan September tahun 2000, paten tersebut berakhir, sehingga saat ini semua orang dapat menggunakannya dengan bebas.
Apa itu algoritma RSA
RSA merupakan algoritma kriptografi asimetri, dimana kunci yang digunakan untuk mengenkripsi berbeda dengan yang digunakan untuk mendekripsi. Kunci yang digunakan untuk mengenkripsi disebut dengan kunci public atau Public Key, dan yang digunakan untuk mendekripsi disebut dengan kunci privat atau Private Key
RSA dikenal juga sebagai salah satu algoritma kriptografi yang menggunakan konsep kriptografi kunci publik. RSA membutuhkan tiga langkah dalam prosesnya, yaitu : pembangkitan kunci, enkripsi, dan dekripsi. Dimana proses enkripsi dan dekripsi merupakan proses yang hampir sama, maksudnya jika bilangan acak yang dibangkitkan kuat, maka akan lebih sulit untuk melakukan cracking terhadap pesan. Parameter yang dijadikan kuat tidaknya suatu kunci yaitu terdapat pada besarnya bilangan acak yang digunakan.
Contoh enkripsi dan dekripsi algoritma RSA
Berikut ini adalah contoh perhitungan manual enkripsi dan dekripsi menggunakkan algoritma RSA.
Dimana sebelum-nya kita harus menentukkan dulu Public Key Dan Private Key nya.
Dan berikut langkah-langkah algoritma RSA mendapatkan Public Key Dan Private Key :
- Pertama, menentukan 2 buah bilangan prima untuk p dan q :
p = 11
q = 13 - Selanjutnya mendapatkan nilai n dimana rumus-nya :
n = p * q
dan akan menjadi seperti ini :
n = 11 * 13
n = 143 - Mendapatkan nilai m dimana rumus-nya :
m = (p - 1) * (q - 1)
dan akan menjadi seperti ini :
m = (11 - 1) * (13 - 1)
m = (10) * (12)
m = 120 - Menentukan nilai e dengan syarat :
e = e > 1 and GCD(m,e) = 1
Dimana "17" adalah nilai yang memenuhi syarat untuk nilai e
e = GCD(120,17) = 1 - Menentukan nilai d dengan syarat :
d = (d * e) mod m = 1
Dimana "473" adalah nilai yang memenuhi syarat untuk nilai d
d = (473 * 17) mod 120 = 1 - Dari proses diatas, maka akan mendapatkan kunci public dan kunci privat dimana :
public key = (e,n)
private key = (d,n)
Dan kunci akan menjadi seperti ini :
public key = (17,143)
private key = (473,143) - Setelah kita mendapatkan public key dan private key, proses selanjutnya melakukan Enkripsi dan Dekripsi,
yaitu kata "INDONESIA". Berikut prosesnya :
Text ASCII
(A)Proses Enkripsi (X)
C = A ^ e mod nProses Dekripsi (Y)
Y = C ^ d mod nI 73 = (7 ^ 17) mod 143 = 50
= (3 ^ 17) mod 143 = 9
= 50.9= (50 ^ 473) mod 143 = 7
= (9 ^ 473) mod 143 = 3
= 73 → IN 78 = (7 ^ 17) mod 143 = 50
= (8 ^ 17) mod 143 = 112
= 50.112= (50 ^ 473) mod 143 = 7
= (112 ^ 473) mod 143 = 8
= 78 → ND 68 = (6 ^ 17) mod 143 = 41
= (8 ^ 17) mod 143 = 112
= 41.112= (41 ^ 473) mod 143 = 6
= (112 ^ 473) mod 143 = 8
= 68 → DO 79 = (7 ^ 17) mod 143 = 50
= (9 ^ 17) mod 143 = 81
= 50.81= (50 ^ 473) mod 143 = 7
= (81 ^ 473) mod 143 = 9
= 79 → ON 78 = (7 ^ 17) mod 143 = 50
= (8 ^ 17) mod 143 = 112
= 50.112= (50 ^ 473) mod 143 = 7
= (112 ^ 473) mod 143 = 8
= 78 → NE 69 = (6 ^ 17) mod 143 = 41
= (9 ^ 17) mod 143 = 81
= 41.81= (41 ^ 473) mod 143 = 6
= (81 ^ 473) mod 143 = 9
= 69 → ES 83 = (8 ^ 17) mod 143 = 112
= (3 ^ 17) mod 143 = 9
= 112.9= (112 ^ 473) mod 143 = 8
= (9 ^ 473) mod 143 = 3
= 83 → SI 73 = (7 ^ 17) mod 143 = 50
= (3 ^ 17) mod 143 = 9
= 50.9= (50 ^ 473) mod 143 = 7
= (9 ^ 473) mod 143 = 3
= 73 → IA 65 = (6 ^ 17) mod 143 = 41
= (5 ^ 17) mod 143 = 135
= 41.135= (41 ^ 473) mod 143 = 6
= (135 ^ 473) mod 143 = 5
= 65 → A
Begitulah proses pembentukan kunci public dan private juga enkripsi dan dekripsi menggunakkan algoritma RSA
Screenshoot Program Proses Enkripsi Algoritma RSA
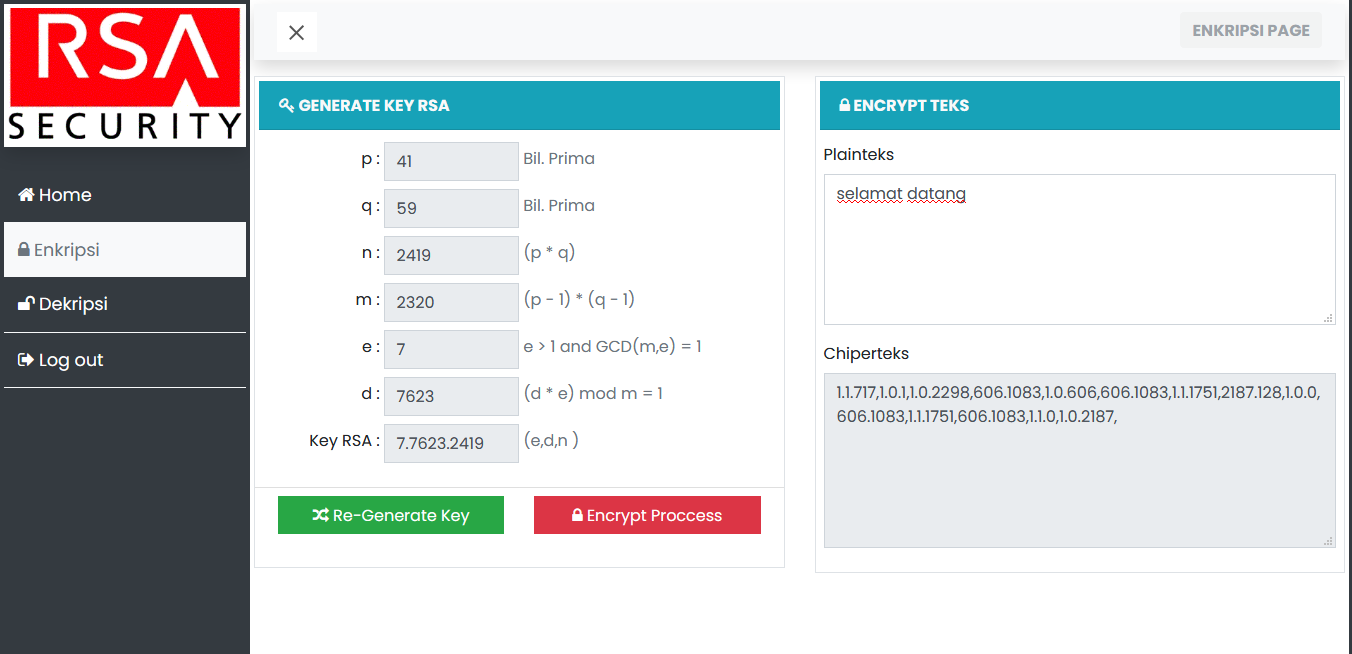
Screenshoot Program Proses Dekripsi Algoritma RSA

Latest Post
Penerapan Metode Bayes Dalam Sistem Pakar
- Algoritma -
Sistem Pendukung Keputusan Menggunakkan Metode AHP
- Algoritma -
Perhitungan Metode Fuzzy AHP Dalam Pemilihan Karyawan Terbaik
- Algoritma -
Tags
Perhitungan RSAPerhitungan Kriptografi RSAPerhitungan Enkripsi RSAPerhitungan Dekripsi RSAPerhitungan Menentukkan Kunci RSAProgram Perhitungan RSADemo Program Perhitungan RSA
About PayahTidur
Jasa Konsultasi Dan Pembuatan Program. Sudah Berpengalaman Lebih Dari 10 Tahun Dalam Dunia
Pemrograman.
Pengerjaan Cepat dan Harga Terjangkau.
Contact : 0813 7027 3471
PayahTidur Products
Sistem Pakar
SPK (Sistem Pendukung Keputusan)
Data Minning
JST (Jaringan Syaraf Tiruan)
Images Proccesing (Pengolahan Citra)
Sistem Informasi Geografis (SIG)
E-Commerce Website
Sistem Informasi
PayahTidur Skills
PHP
Microsoft Visual Studio
Android Mobile
JST (Jaringan Syaraf Tiruan)
Maps Google
Laravel Framework / CI Framework
Matlab
Java